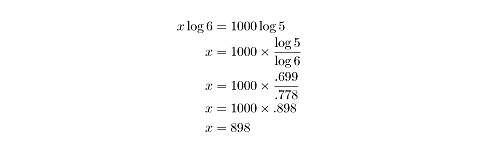Logarithms have important uses in solving problems with complicated exponential equations. Consider the following example:
The population of a small town is 1000 on January 1, 2001. It grows at a constant rate of 2% per year. In what year does the population of the town first exceed 1500?
This question is like the exponential growth problems we’ve just seen but with a twist. Here, we’re given the growth rate, the initial quantity, and the ending quantity. We need to find the number of percent changes (in this case, the number of years) that links all these values. Since logarithms are the power to which you must raise a given number to equal another number, they are the perfect tool for solving this sort of problem.
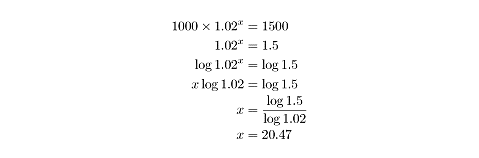
In this case, it will take roughly 20.5 years for the town’s population to exceed 1500. So about halfway through the year 2021, the population will first exceed 1500. The general form for a problem like this one, in which the exponent is unknown, is to isolate the exponential term, take the logarithm of both sides, and then use the power rule of logarithms to bring the variable out of the exponent. You can then isolate the variable on one side of the equation. The base of the logarithms is insignificant. You could choose a base-10 logarithm or a logarithm of any other base, as long as it is consistently used. Here’s a simple example to illustrate this process:
If 6x = 51000, then find the value of x.
This problem would be vastly more difficult if we didn’t have logarithms. How would you possibly calculate 51000 anyhow? And how do you solve for x when it’s the exponent of a number? But by taking the logarithm of each side of the equation, and utilizing the power rule of logarithms:
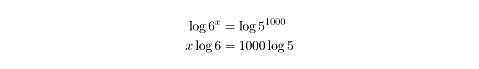
The confusion clears, and we see that we have a logarithm problem that can be methodically solved.