
P1(微分几何函数求解)

本题考查的分别是第二章二次函数如何求解,第五章如何求直线方程以及两直线垂直斜率相乘得-1这个知识点,还有第八章微分的几何意义:导数的几何意义就是曲线上某点处切线的斜率。通过微分求出斜率求出切线方程。也就是说这道题其实没有单纯的考一个知识点或者一个章节,而是从三个章节中选出常考的知识点进行结合,这也是我们在考试中经常会出现的考法:多个章节的知识点结合出题。
那么a问就是证明P点在曲线C上,只需要证明P点的x,y坐标可以满足曲线方程就好,因为它既然在曲线上就是C上无数个点中的一员,所以我们需要做的就是将P点的坐标带入进曲线的方程里。b问要求的是曲线上P点的切线,既然要求直线就要知道直线的方程,利用点斜式直线方程(点斜式方程只需要一个点和斜率,这里我们已知P点坐标,只再需要一个斜率就好),求斜率,斜率的求法就是根据我们微分一章学到的几何意义,求导得到的就是曲线上任意一点的斜率,无数个点有无数个切线以及斜率,区别的点就在于点的坐标,所以我们将P点坐标带入到求出的导数里面就可以求出该条切线的斜率,最后连同P点带入到直线方程,得到tangent(切线)。最后一问给了额外的条件:曲线C上Q点的切线和P点的切线垂直,读到这句话就可以得出两直线的斜率关系:相乘得-1。根据P切线的斜率得到Q直线的斜率,那么前面我们提到斜率就是曲线的导数,所以我们只需要利用求完的导数和P的导数互为负导数就可以了,最后得都Q点的横坐标。

该学生a问是按照老师的要求去把点带入到曲线里了,b问也是先通过求导带入点进去得到斜率,再把斜率点带入到直线就可以了。所以这两问都得到分数了,最后一问就是对于二次函数以及导数的定义不够清晰,所以不会求解。

该学生解题思路清晰且步骤书写工整,说明对题目理解比较到位,所以得分也比较容易。
P2 (数列应用题)

这是P2的一道关于数列的应用题,需要同时掌握等差等比数列的公式应用,同时这是在纯数里面对英文要求相对较高的一道题目。
首先Model 1是每天比前一天增长1000,所以这是一个等差数列,因为我们要得到前40天的总额,所以我们用到的是求和公式。
Model 2 是每天相对前一天增长10%,这就是一个等比数列,但是要注意的是我们在用公式的时候其中的r是110%,即需要考虑到本身是有1倍,增加10%,就是原来的1.1倍。
但是这题的最后我们要审题,因为我们要把总额的5%捐出去,所以最后要乘一下。
下面我们来看一下学生的答题情况
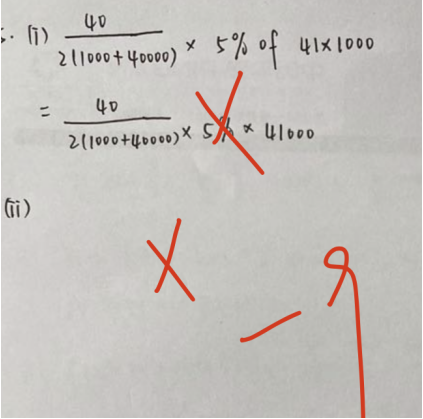
位同学很明显没有理解公式怎么用,我们等差等比求和公式分别如下:
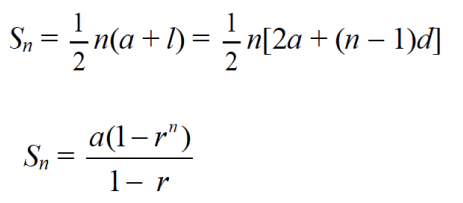
Model1中 n是天数:40,a为天的钱:1000,d为每天增加的数:1000。把每个数值带入变量即可求出前40天总和。
Model2中其他变量一样,r为增长比例是1.1
最后分别乘以5%就是最后结果。

第二位学生表现的就比较好,但是在最后等比的计算中我们的n还是40,学生写成了39。
在这类题目计算时,大家要注意先运用求和公式再乘以5%,这样不容易出错。
学生在考试中需要注意审题,计算要仔细,如果时间充分,检查多次,避免失误。






